Gradient Descent Intuition

Since the past few weeks I have been taking the certificate course on machine learning taught by Andrew Ng. Even though I had taken the free version of this course way back during college, some aspects of it eluded me at that time. This was because the scripts used in this course are written to work with octave and since the language was not part of my curriculum I skipped some of the practical assignments and simply skimmed through the theory.

Recently, I thought it would be a good exercise to go through the course once again and try to understand all its nuances. One way of doing this was to implement all the assignments in R without using any library. Following is my attempt at understanding gradient descent. Complete codes for this exercise can be found here.

Gradient Descent - Intuition

What exactly is a Gradient?

Recalling the equation of a straight line:

Rewriting this in a slightly different form (used by Prof. Ng in his lectures) we get:

Here \( \theta \) is the gradient analogous to slope m in the equation of a line. If I recall, the slope of a line in a 2D plane it is calculated as \( \frac{y_2 - y_1}{x_2 - x_1} \) i.e. by how much will y change if x is changed by a certain amount?

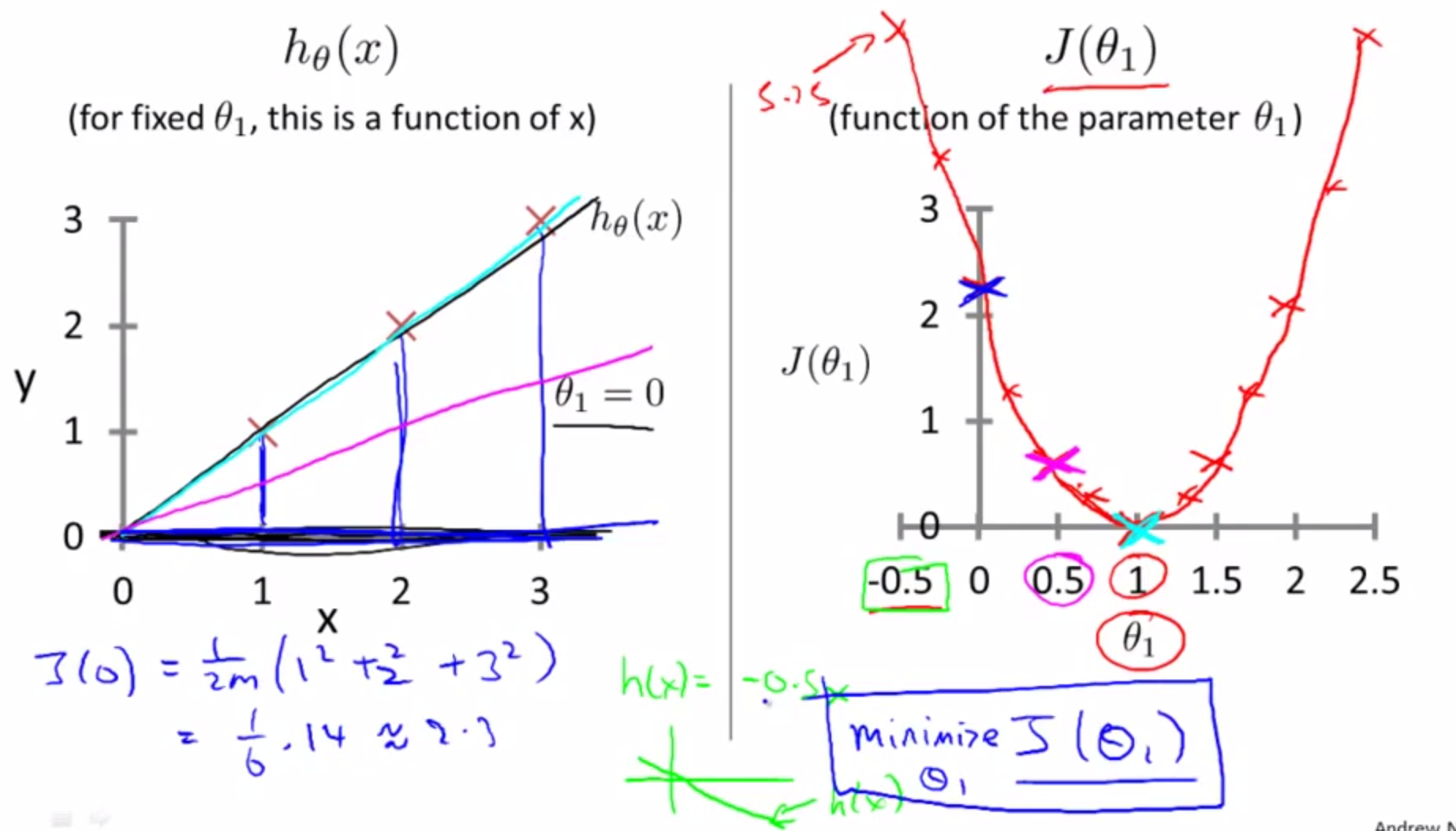
Now I want to fit a line through my data in such a way that it passes through majority of the points. So that in the future if I want to predict the position of an unknown point I can just use the line I used to fit my data. What I want is that the line that I am trying to fit exactly traces my data points so that the distance (error in machine learning culture) between my fitted line and data points is minimum. To do this I need to understand that by how much (magnitude) and in what direction I need to change the slope of my line so that it fits majority of my data points.

What is a cost function?

This is where the cost function \( J(\theta) \) comes into picture. Cost is simply the distance (error) between my data points and fitted line and ideally this must be as close to 0 as possible. By taking its partial derivative I calculate how much (magnitude) cost will change if I change \( \theta \) by a certain amount (this is the same logic which is used for calculating slope of a line, i.e. magnitude of change in y with respect to x. And also a general idea of calculus which deals with the mathematics of change of one quantity with respect to another.)

What is descent in gradient descent?

Getting an idea of the cost function and gradient I move on to the descent in gradient descent. The central idea here is that I want to find the optimum value of \( \theta \) so that my cost \( J(\theta) \) is as low as possible (close to zero). To do this I have to iterate over different values of \( \theta \). This change in value of \( \theta \) is done using the learning rate/step or \( \alpha \) which is nothing but a small multiplication factor (0 to 1). The gradient (partial derivative of \( J(\theta) \)) always points in the direction of the steepest ascent i.e. - in the direction where change in cost is maximum. But since I want my cost to be minimum I go in the opposite direction or towards a descent. With each step the gradient is recalculated and I move towards the opposite direction and possibly reach a global minima. This minima is the lowest possible value that can be obtained for the function \( J(\theta) \) given a value of \( \theta \).

Why gradient points in the direction of steepest ascent?

Recalling some basic vector calculus I know that the dot(.) product between 2 vectors equals:

Here the quantity can be maximum only when \( cos\theta \) is 1. Which is only possible if \( \theta \) is 0. i.e. both a and b are in the same direction. Extending this argument further, if we consider \( grad(f(a)) \) as a vector and an arbitrary unit vector \( v \), we can project along this direction using the dot product \( grad(f(a)).v \), which is also the definition of a directional derivative. And this dot product will be maximum only when both vectors are in the same direction.